Björling's Problem and DPW for Willmore Surfaces

(Joint work with Peng Wang)

Björling's classical problem for minimal surfaces is to find a minimal surface containing a given curve with the surface normal prescribed along the curve. There is a unique solution using the Weierstrass-Enneper representation. Minimal surfaces are local minimizers of the area functional, and are characterized as having zero mean curvature $H$. Willmore surfaces are a generalization of minimal surfaces: they are local minimizers of the Willmore energy $$\int_S H^2 dA.$$ This property is invariant under conformal transformations of the ambient space. If you replace isometries with conformal maps, thus working in conformal geometry, then all the space forms are locally equivalent, and in fact you have ${\mathbb H}^n \subset {\mathbb R}^n \subset {\mathbb S}^n$. From the conformally invariant point of view, the study of Willmore surfaces is really the study of Willmore surfaces in the 3-sphere ${\mathbb S}^3$, and these surfaces are a conformal analogue of minimal surfaces.

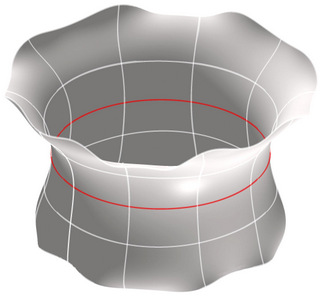Example 1

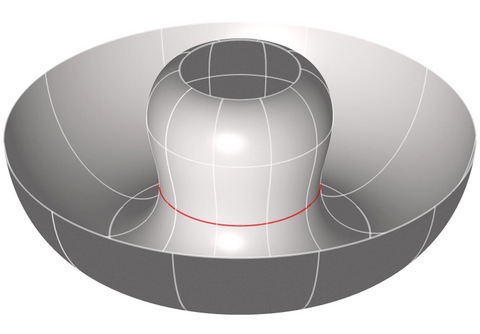Example 2

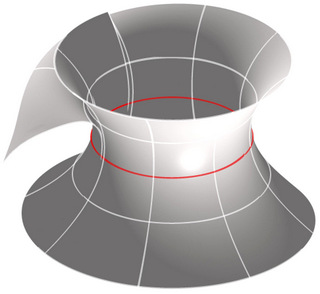Example 3

Sphere Congruence

Given the prescription of a curve and surface normal along the curve, there is not a unique solution to the Björling problem for the case of Willmore surfaces: see the three examples above. However, in Möbius geometry (conformal geometry of the 3-sphere), an analogue for the surface normal is the conformal Gauss map. Everything is lifted to the Minkowski 5-space ${\mathbb R}^{1,4}$. A map $y$ into ${\mathbb S}^3$ is lifted to a map $Y$ into the light cone of ${\mathbb R}^{1,4}$. The conformal Gauss map $\psi$ is a spacelike unit vector orthogonal to $Y$ and its derivatives. For Willmore surfaces, there is a dual surface $\hat Y$, found by Robert Bryant (J. Differential Geom. 20 (1984), no. 1, 23-53), with the same conformal Gauss map $\psi$. The map $\psi$ is called a sphere congruence, because it corresponds to a family of 2-spheres in ${\mathbb S}^3$, and $y$ and $\hat y$ are enveloping surfaces - they are both tanget to the corresponding 2-sphere at corresponding points (see image above).

It turns out that, given a curve $Y(u,0)$, prescribing the dual surface $\hat Y(u,0)$ and the conformal Gauss map $\psi(u,0)$ along the curve are sufficient to determine a unique Willmore surface $y(u,v)$, and this we consider to be the analogue of Björling's problem in conformal geometry.

In the reference below, we solve this problem using a generalized Weierstrass representation, based on the DPW method for harmonic maps of Dorfmeister, Pedit, and Wu, (Comm. Anal. Geom. 6 (1998), no. 4, 633-668). We use the construction given by Frédéric Hélein (J. Differential Geom. 50 (1998), no. 2, 331-385), which exploits the harmonicity of the map $Y \wedge \hat Y$, where $Y$ is a lift of the surface to the light cone in the Minikowski 5-space, and $\hat Y$ the lift of the dual surface. We give explicit formulae for the potentials of the solution in terms of the prescribed geometric data. The solutions can then be computed numerically from these potentials. Some images we computed are at the links below.

A numerical implementation that computes the solution from the prescribed data on a curve can be found here.